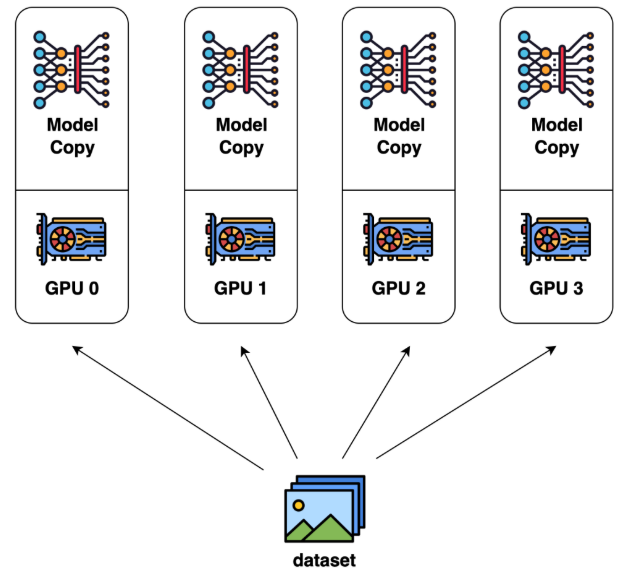
数据并行 Data Parallel
在深度学习领域,训练往往需要处理海量的数据与庞大的数学运算:大模型有数亿甚至数百亿参数,大规模数据集常常包含数千万甚至上亿样本。一个模型的训练动辄要几天甚至几周,如果只靠一张GPU或一台服务器,训练速度就太慢。此时就需要分布式训练,而数据并行是最常用也最有效的方式:既然一张GPU跑得慢,就让多张GPU并行跑;一台机器不够快,就用多台机器同时跑。
数据平行将数据集划分为$N$份,每一份分别分配到$N$个GPU节点上。每个GPU节点持有一个完整的模型副本,分别基于每个GPU中的数据去训练。在每一轮迭代中,各GPU分别进行前向传播和反向传播、独立计算出梯度,随后所有GPU节点之间通过梯度同步机制(例如AllReduce、Parameter Server)交换并平均梯度,以保证所有设备上的模型参数保持一致,进而可以进行下一轮操作。这样就能通过多台设备同时处理更大规模的数据,有效提升训练速度。
模型并行 Model Parallelism
传送门:模型划分及并行 - CSDN博客
在大规模深度学习模型中,模型参数数量往往达到数十亿甚至数千亿级别,单张GPU的显存无法容纳整个模型及其梯度与优化器状态,传统的数据并行方法因此面临显存瓶颈与扩展性限制。为解决这一问题,模型并行将同一个神经网络按照不同维度切分成多个子模型,并将这些子模型分配到不同的计算节点上共同完成前向与反向计算。因此每个节点只计算模型的一部分,但需要频繁的设备间通信来传递中间结果。模型并行能够有效打破单卡显存的限制,使训练超大规模模型成为可能,并在实际工程中常与数据并行结合,构建可扩展的分布式训练系统。
常用的模型划分方法有横向按层跨分、纵向跨层划分、混合划分以及模型随机划分。
横向按层跨分
横向按层划分是将模型按照层次结构进行切分,每个子模型可以由一个或多个连续的网络层构成,并分别部署在不同的计算节点上。在训练或推理过程中,数据按照模型的拓扑结构顺序流经各个节点:每个节点完成其所负责子模型的前向或反向计算后,将中间结果传递给下一个节点。节点之间通过通信机制、计算依赖关系交换必要的中间激活和梯度,实现跨节点的协同计算。具体而言,在前向传播时,每一个节点要先向前一个节点请求获取首层的数据,完成子模型的计算后,再把数据存到末层上,供下一层节点请求数据。在反向传播时,每个节点要先向后一个节点请求误差,经过训练后将误差供前一个节点请求误差值。

纵向跨层划分
纵向跨层划分是指将模型中每一层的参数按一定规则均匀切分为若干部分,并分别分配到不同计算节点上。每个节点因此拥有整个神经网络的结构副本,但仅存储各层中属于本节点的部分参数及与之关联的神经元连接信息。在训练或推理过程中,当节点需要访问本地未存储的神经元值或梯度时,需要向其他节点发起请求以获取相关数据,从而实现跨节点的协同计算与参数更新。

混合划分
如果每层的神经元数目不多而层数较多,可以考虑横向按层划分。如果每层的神经元数目很多而层数较少,则应该考虑纵向跨层划分。如果神经网络层数和每层的神经元数目都很大,则需要结合使用横向按层划分与纵向跨层划分,即混合划分。

随机模型划分
由于神经网络本身具有一定的冗余性,一个复杂网络中通常存在规模更小、性能相近的子网络,这样的网络被称为骨架网络。随机模型划分方法基于骨架网络设计:首先由中央服务器从完整模型中选出骨架网络,并将其分发到各工作节点;每个节点除了存储骨架网络,还随机选择部分非骨架神经元及其连接,以探索骨架网络之外的全局拓扑信息。各节点基于本地数据独立训练后,将梯度或误差信息上传至中央服务器进行聚合,并周期性地重新选择新的骨架网络以持续优化。
骨架网络的选取流程通常为:中央服务器首先根据每层神经元在其出边上的权值绝对值之和,贪心选取前$(a-b)%$的神经元;随后再随机选择剩余神经元中的$b%$ 加入骨架网络,使其兼具确定性与随机性。在训练后,各节点根据误差值及边权绝对值选取贡献度最大的$(a-b)%$误差信息,并随机补充$b%$误差值发送给服务器进行全局聚合。

流水线并行 Pipeline Parallel
传送门:
分布式机器学习里的 数据并行 和 模型并行 各是什么意思?- 知乎
流水线并行论文总结 - 知乎
GPipe: Efficient Training of Giant Neural Networks using Pipeline Parallelism
PipeDream: Fast and Efficient Pipeline Parallel DNN Training
最朴素的模型并行方式(横向按层跨分)将模型按层划分后,不可避免地面临前后层之间的顺序依赖:后面的GPU必须等待前面GPU的输出作为输入,导致大量GPU在等待时处于空闲状态,这部分空闲时间被称为气泡(bubbles),严重影响计算资源利用率和训练速度。
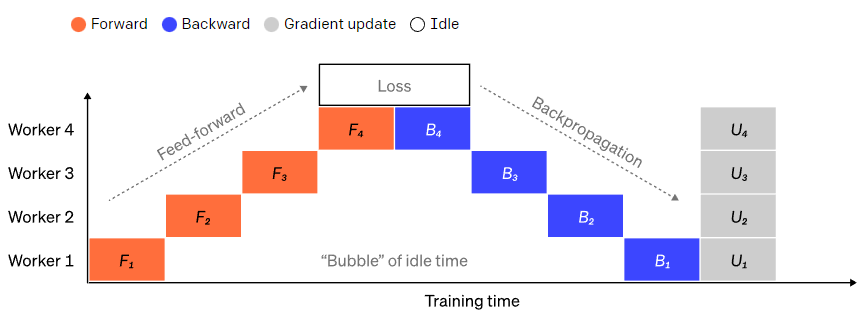
为了降低因依赖带来的空闲,流水线并行引入了分批次调度的思想:将一个大批次(batch)切分为多个更小的微批次(micro-batches),各个GPU可以同时处理不同的微批次数据,从而在一个GPU等待时,其他GPU可以继续计算新的数据。这样显著提高了硬件利用率,减少了等待带来的性能损失。因此流水线并行是一种特殊形式的模型并行(横向按层跨分)。
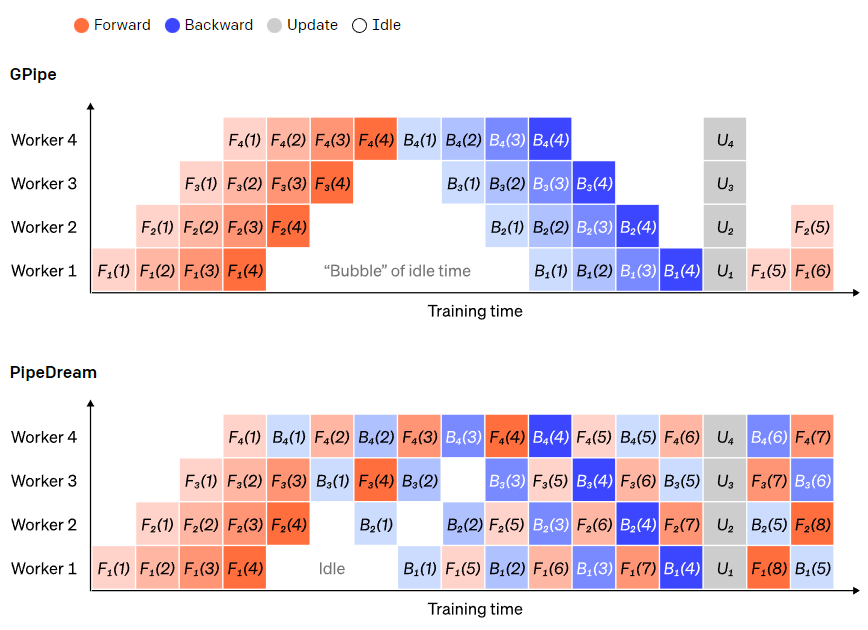
具体而言,在GPipe的流水线并行中,当GPU1完成第一个微批次的前向传播后,GPU2就可以立即接收GPU1的输出并开始对同一个微批次进行前向传播。与此同时,GPU1则可以继续处理第二个微批次的前向传播。这样多个GPU之间就形成了类似装配线的流水式处理。在反向传播阶段也是类似,当 GPU4完成第一个微批次的反向传播并将梯度传递给 GPU3后,GPU4可以立即开始对第二个微批次进行反向传播。因此GPipe在保持模型并行的同时,也引入了类似数据并行的批次切分思想,通过切分数据提高流水线并行度,减少了GPU的空闲时间,从而实现更好的硬件利用率和训练加速。
GPipe需要等所有的微批次前向传播完成后,才会开始反向传播。PipeDream则是当一个微批次的前向传播完成后,立即进入反向传播阶段。在该模式下,前向计算和反向计算交叉进行,可以及时释放不必要的中间变量,降低了对显存的需求。因此在梯度更新上,Gpipe是同步的,PipeDream是异步的。
张量并行 Tensor Parallelism
传送门:
Megatron-LM: Training Multi-Billion Parameter Language Models Using Model Parallelism
wdndev/llm_interview_note/04.分布式训练/4.张量并行/4.张量并行.md- Github
在训练非常大的模型(比如 GPT-3 这种百亿参数规模)时,即使只考虑模型中的某一层,里面的参数矩阵也可能大到单个GPU无法完全存储或高效计算。张量并行的核心就是:不是简单地把不同层放在不同GPU上,而是把同一层中的参数张量(比如权重矩阵)本身切分成几块,让每个GPU各计算自己负责的那一块。因此张量并行与流水线并行一样同属于模型并行。
以通用矩阵的矩阵乘法为示例,假设$Y = X A$ ,其中$X$是输入、$A$是权重、$Y$是输出。

行并行就是把权重$A$按照行分割成两部分,同时把输入$X$按照列来分割为两部分。在GPU0上可以基于$X_1$和$A_1$计算得出$Y_1$,在GPU1上可以基于$X_2$和$A_2$计算得出$Y_2$,最后把$Y_1$和$Y_2$结果相加即可得到最终的输出$Y$。
$$ \begin{aligned} Y = XA &= \begin{bmatrix} X_1 & X_2 \end{bmatrix} \begin{bmatrix} A_1 \\ A_2 \end{bmatrix} \\ &= X_1 A_1 + X_2 A_2 \\ &= Y_1 + Y_2 \\ &= Y \end{aligned} $$列并行就是把权重$A$按列分割成两部分。在GPU0上可以基于$X$和$A_1$计算出$Y$的一部分,在GPU1上可以基于$X$和$A_2$计算出$Y$的另一部分,最终将2个GPU上面的矩阵拼接在一起,得到最终的输出$Y$。
$$ \begin{aligned} Y = XA &= X \begin{bmatrix} A_1 & A_2 \end{bmatrix} \\ &= \begin{bmatrix} X A_1 & X A_2 \end{bmatrix} \\ &= \begin{bmatrix} Y_1 & Y_2 \end{bmatrix} \\ & = Y \end{aligned} $$上述过程中将$Y_1$与$Y_2$相加与拼接,即在GPU之间做一次AllReduce操作与AllGather操作。
序列并行 Sequence Parallelism
自注意力机制
传送门:
Transformer & BERT
Self-attention 自注意力机制讲解 李宏毅版 v.s 吴恩达版 - 知乎
大语言模型无法直接理解完整的句子或段落,需要把输入的内容先切割成许多小的部分,然后作为一个向量序列输入模型处理。向量序列中的不同向量之间存在一定的关系,若无法充分利用这些输入之间的关系,会导致模型训练结果效果极差。因此自注意力机制能够捕捉序列中不同元素之间的依赖关系,并根据这些依赖关系生成新的序列表示。对于每一个输入向量$a$,经过蓝色部分self-attention之后将输出一个向量$b$。例如对于这个向量输入向量$a^1$,在考虑了和各输入向量$a^1$、$a^2$、$a^3$、$a^4$与$a^1$的关联度后将得到输出向量$b^1$。以此类推,输入向量序列$a^1$、$a^2$、$a^3$、$a^4$进处理后将输出向量序列$b^1$、$b^2$、$b^3$、$b^4$。

计算关联度$\alpha$有很多方法,Transformer采用的是Dot-Product方法:
- 当前的输入向量$a^i$称之为query,它对应有权重矩阵$W^q$,query向量为权重矩阵$W^q$乘以输入向量$a^i$,即$q^i = W^q a^i$;
- query外的其它输入向量$a^j$则被称为key,其对应有权重向量$W^k$,key向量为权重矩阵$W^k$乘以输入向量$a^j$,即$k^j = W^k a^j$;
- 输入向量$a^i$(query)和输入向量$a^j$(key)的关联度$\alpha_{i,j}$是二者的点积,即$\alpha_{i,j} = q^i k^j$。

例如计算$a^1$(query)和$a^2$(key)的关联度:$q^1 = W^q a^1$、$k^2 = W^k a^2$、$\alpha_{1,2} = q^1 k^2$。类似的,输入向量$a^1$将依次和$a^1$、$a^2$、$a^3$、$a^4$得到关联度$\alpha_{1,1}$、$\alpha_{1,2}$、$\alpha_{1,3}$、$\alpha_{1,4}$。随后即可通过激活函数(例如Soft-max函数)输出激活后的$\alpha^{\prime}_{1,1}$等,也就是所需要的注意力权重。

最后依据注意力权重计算出最终的$b^1$:
- 对于每一个输入向量$a^j$基于权重矩阵$W^v$可计算出向量$v^j = W^v a^i$;
- 依据注意力权重$\alpha^{\prime}_{1,j}$和向量$v^j$加权求和即可得出最终的$b^1$,也就是说谁和当前向量的关系越大,其信息就越会被抽取出来。

依据上述步骤可同理可计算出$b^2$、$b^3$、$b^4$,并可归纳为矩阵运算:
- 计算出注意力权重矩阵:$A = softmax(QK^T/\sqrt{d_k})$
- 计算加权和:$B=AV$
下图为简化版的矩阵运算,因此所示公式与下图存在一些差异。其中的$\sqrt{d_k}$表示向量的维度,是为了缩放点积结果,进而使注意力分布更加平滑。


Colossal-AI
传送门:Sequence Parallelism: Long Sequence Training from System Perspective
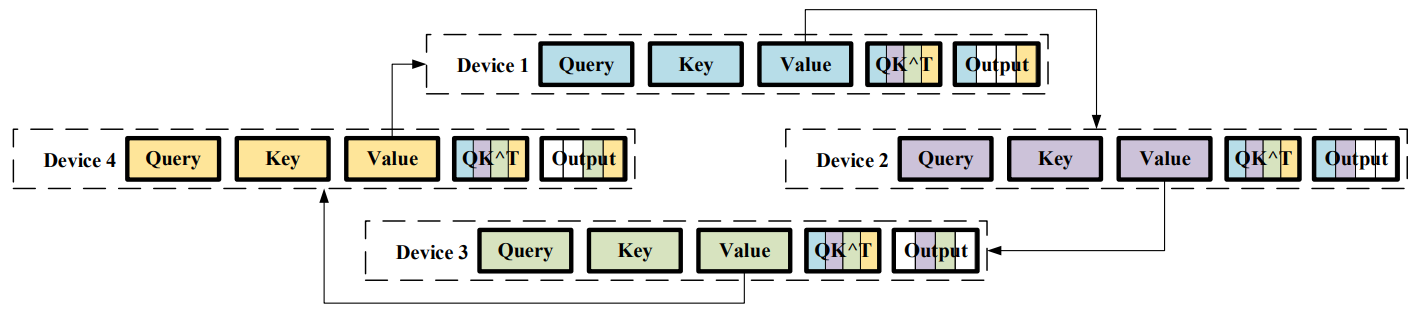
为解决模型的序列长度限制,Colossal-AI将输入序列分割成多个块,并将每个块输入到其相应的GPU中,因此不再需要单个GPU设备来保存整个序列。

- 第一次迭代:
- GPU1从GPU4接收到$K_4$,因此可以计算出$Q_1 K_4$
- GPU2从GPU1接收到$K_1$,因此可以计算出$Q_2 K_1$
- GPU3从GPU2接收到$K_2$,因此可以计算出$Q_3 K_2$
- GPU4从GPU3接收到$K_3$,因此可以计算出$Q_4 K_3$
- 第二次迭代:
- GPU1从GPU4接收到$K_3$(在第一次迭代中,GPU4从GPU3获得),因此可以计算出$Q_1 K_3$
- GPU2从GPU1接收到$K_4$(在第一次迭代中,GPU1从GPU4获得),因此可以计算出$Q_2 K_4$
- GPU3从GPU2接收到$K_1$(在第一次迭代中,GPU2从GPU1获得),因此可以计算出$Q_3 K_1$
- GPU4从GPU3接收到$K_2$(在第一次迭代中,GPU3从GPU2获得),因此可以计算出$Q_4 K_2$
- 在进过几轮迭代后,通过对$K_1$、$K_2$、$K_3$、$K_4$的传递:
- GPU1会持有$Q_1 K_1$、$Q_1 K_2$、$Q_1 K_3$、$Q_1 K_4$,即$Q_1 K$
- GPU2会持有$Q_2 K_1$、$Q_2 K_2$、$Q_2 K_3$、$Q_2 K_4$,即$Q_2 K$
- GPU3会持有$Q_3 K_1$、$Q_3 K_2$、$Q_3 K_3$、$Q_3 K_4$,即$Q_3 K$
- GPU4会持有$Q_4 K_1$、$Q_4 K_2$、$Q_4 K_3$、$Q_4 K_4$,即$Q_4 K$
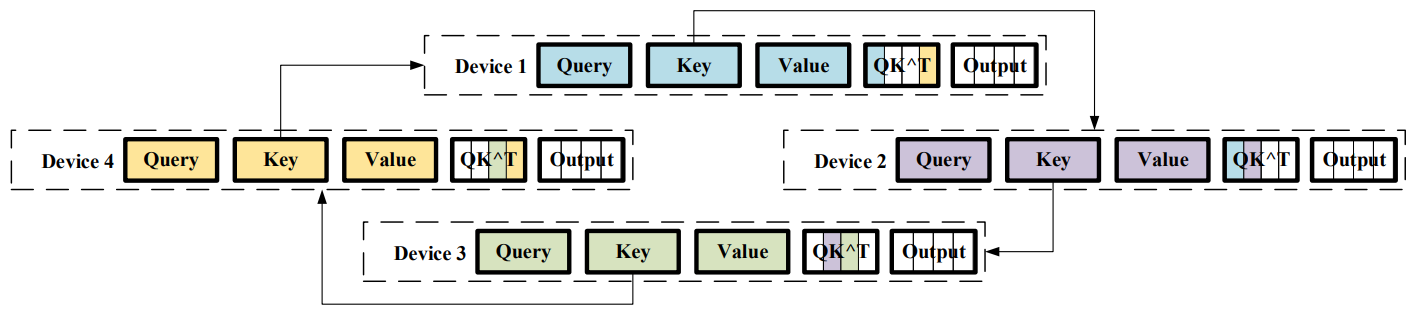
接下来计算加权和也是类似的逻辑,GPU之间通过类似Ring Allreduce的机制传输各自的$V$,通过计算得到最终的输出。
多头自注意力机制
图示在自注意力机制的基础上,将Dot-Product过程做$H$次,最后再把输出合并起来。这种机制称为多头注意力机制,通过将模型分为多个头、形成多个子空间,可以让模型关注不同方面的信息。叠加序列并行的计算过程如下:
- 分别计算每个头:$head_i = Attention(Q W_i^Q, K W_i^K, V W_i^V)$
- 将各个头的结果拼接在一起:$MultiHead(Q,K,V) = Concat(head_1, head_2, … ,head_h) W^O$

DeepSpeed Ulysses
传送门:
图解大模型训练系列:序列并行2,DeepSpeed Ulysses - 知乎
DeepSpeed Ulysses: System Optimizations for Enabling Training of Extreme Long Sequence Transformer Models
在多头注意力机制的场景下,DeepSpeed-Ulysses针对Colossal-AI进行了优化,通过All-to-All的通信操作序列切分转变为对头的均分,避免了类似Ring Allreduce的高时延过程。流程如下:
- 序列切分:将长度为$N$的输入序列均匀切分为$P$个长度为$N/P$子序列,分别装配到$P$个GPU上;
- 本地计算$Q_j$、$K_j$、$V_j$:第$j$块GPU基于持有的第$j$段子序列,计算出该子序列对应的$Q_j W_Q$、$K_j W_K$、$V_j W_V$,注意这里的$W_Q$、$W_K$、$W_V$是全部头的完整矩阵,因此得到的是第$j$段子序列、全部头的计算结果;
- 从序列切分转变为头切分:通过All-to-All通信,使得第$i$块GPU拿到第$i$个头、完整序列的$Q_i$、$K_i$、$V_i$,即GPU1、GPU2、……、GPU P分别将子序列1、子序列2、……、子序列P的第0个头的计算结果传输给GPU0,GPU0进而获得第0个头的完整序列;
- 计算Attention:每张GPU持有完整序列的部分头,因此每张GPU能够独立计算出所负责头的Attention结果;
- 还原结果:为完成后续的拼接,需要再次通过All-to-All通信,还原为原先按照序列切分的布局,此时每张GPU持有所负责子序列的所有头输出;
- 得出最终结果:每张GPU针对所持有的子序列,基于所有头输出独立拼接出最终结果。

All-to-All的通信实际上等价于下图所示的矩阵的转置,因此第一次转置让每张GPU可以独立计算Attention(计算Attention需要全序列),第二次转置Attention输出以拼接所有头(需要同一个子序列上的所有头)。
专家并行 Experts Parallelism
MoE
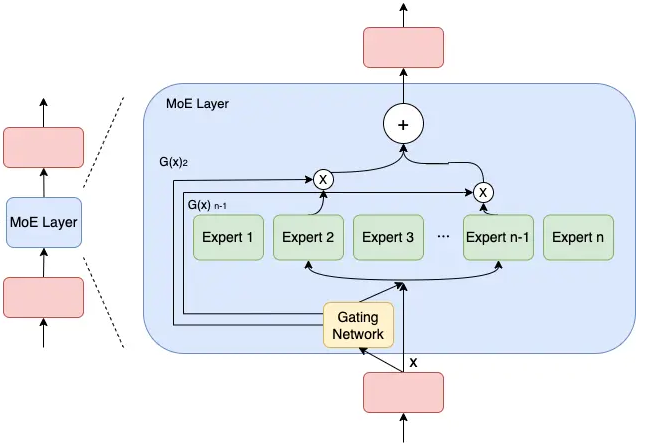
模型规模的扩展会导致训练成本显著增加,计算资源的限制成为了大规模密集模型训练的瓶颈。为了解决这个问题,一种基于稀疏MoE层的深度学习模型架构被提出,MoE将模型的某一层扩展为多个具有相同结构的专家网络,每轮迭代根据样本决定激活一部分专家用于计算(通过门网络决定激活哪些专家网络用于计算),达到了节省计算资源的效果。
MOE的几种并行方式
在数据并行的部署方式中,门网络和专家网络都被完整地放置在各GPU上,该方式会导致专家的数量受到单个GPU显存大小的限制。


流量分析
传送门:UB-Mesh: a Hierarchically Localized nD-FullMesh Datacenter Network Architecture
| Parallelism Techniques | Communication Pattern | Data Volume Per Transfer | Total Transfer | Total Volume | Data Traffic |
|---|---|---|---|---|---|
| DP | AllReduce | 711.75 MB | 64 | 44.48 GB | 1.34% |
| PP | P2P | 192 MB | 26 | 4.875 GB | 0.14% |
| TP | AllReduce | 360 MB | 4992 | 1775 GB | 52.9% |
| SP | AllGather | 180/360 MB | 4992/1664 | 1462.5 GB | 44.08% |
| EP | AlltoAll | 10.5 MB | 4992 | 51.19 GB | 1.54% |
数据并行(Data Parallelism, DP):
- 每个GPU拿到同一个模型的副本,但处理不同的数据子集;
- 为了同步梯度,GPU之间需要进行AllReduce通信操作;
- DP的流量虽然只占不到2%,但需长距离传输,同时可与计算部分掩盖,需控制通信开销占比。
流水线并行(Pipeline Parallelism, PP):
- 将模型的不同层分配到不同的GPU上处理,并通过流水线填补气泡;
- 涉及用于跨层传输参数的P2P通信;
- 通信量小、通信次数少,可通过流水掩盖,对网络诉求较低。
张量并行(Tensor Parallelism, TP):
- 将单个数学运算(如矩阵乘法)拆分到不同的GPU上运行;
- 主要涉及AllReduce操作以合并结果(也可能包括AllGather操作);
- 通信主要发生在8-64个相邻GPU组成的集群内,属于短距离通信;
- 张量并行所需的通信量最大,且不可被计算掩盖,因此需在同一个服务器内使用张量并行。
序列并行(Sequence Parallelism, SP):
- 将输入序列分割到不同的GPU上执行;
- 需要采用AllGather操作,以收集拼接结果;
- 通信主要发生在8-64个相邻GPU组成的集群内,属于短距离通信;
- 序列并行所需的通信量也很大,,因此需在同一个服务器内使用序列并行。
专家并行(Experts Parallelism, EP):
- 只用模型每一层中的一小部分来处理数据;
- 例如将需要给专家1计算的数据收集起来放在专家1处、将需要给专家2计算的数据收集起来放在专家2处,因此需要使用All-to-All通信;
- 单次通信量小,但通信次数多。
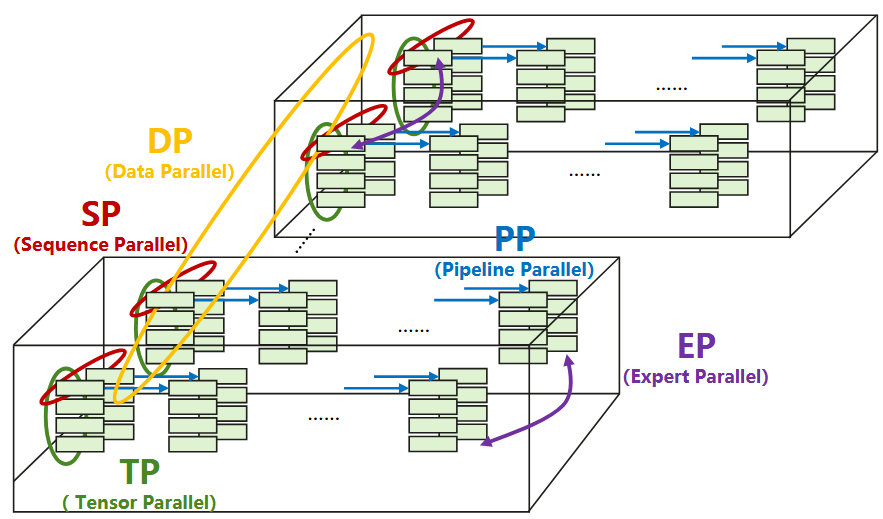
因此存在以下特征:
- 空间局部性:TP和SP的通信主要发生在8-64个相邻GPU组成的集群内,属于短距离通信;而DP等仅占2%的流量需长距离传输;
- 流量分层性:高占比流量TP和SP对带宽需求高但范围局部,低占比流量DP和EP需长距离但带宽需求低。
